EL GRAFENO: ASDRÚBAL VALENCIA GIRALDO Profesor del Departamento de Ingeniería Metalúrgica y de Materiales, Universidad de Antioquia, Calle 67 No 53-108, Bl. 18 of 134 Ciudad Universitaria, Medellín, Colombia. Teléfono 219 55 43
e-mail: avalen@udea.edu.co
RESUMEN El premio nobel de física 2010 fue otorgado a unos investigadores de materiales por su aislamiento del Grafeno; la rapidez con que se hizo este reconocimiento habla de la importancia de este material. En el presente artículo se hace una reseña sobre su origen, su clasificación, características estructurales, propiedades químicas, físicas, mecánicas y tecnológicas. Se indican también algunas de las aplicaciones en que se está usando, las variantes que se investigan y las nuevas posibilidades que se exploran para el grafeno y sus derivados.
PALABRAS CLAVE: Materiales de ingeniería, formas del carbono, grafeno, materiales compuestos propiedades de los materiales.
ABSTRACT Nobel Prize of Physics was awarded to two materials researchers for their isolation of graphene; the speed to recognize this founding shows the importance of such material. In this paper a brief presentation is made of its origin, classification, structural characteristics, chemical, physical, mechanical and technological properties as well as some actual applications. Also new variants are mentioned and the new possibilities that are being explored for graphene and its products.
KEY WORDS: Engineering materials, carbon forms, graphene, composite materials, materials properties.
1. INTRODUCCIÓN El premio Nobel de Física 2010 fue otorgado conjuntamente a André Geim y Konstantin Novosolev “por sus experimentos pioneros con el material bidimensional grafeno”. Geim nació en 1958 en Sochi, Rusia, es decir apenas va a cumplir 52 años, actualmente es ciudadano holandés y trabaja en el Instituto de Materia Condensada de la Universidad de Mánchester, Inglaterra. Konstantin Novoselov también es ruso pero es más joven aún, pues nació en Nizhny Tagil, en 1974 y trabaja en el mismo instituto que su compañero.
Figura 1. Andre Geim y Konstantin Novoselov ganaron el premio Nobel de Física en 2010 por su trabajo con el grafeno. Fuente: http://www.csmonitor.com/Science/2010/1005/Konstantin-Novoselov-and-Andre-Geim-get-Nobel-Prize-for-super-strong-graphene El hecho de que a estos científicos se les haya otorgado el premio Nobel de Física 2010 por un descubrimiento que hicieron en 2004, indica claramente la importancia de este material, que cada día encuentra más aplicaciones por sus sorprendentes propiedades. Por esa razón es pertinente reseñar acá el origen, estructura y propiedades del grafeno así como sus posibilidades tecnológicas.
2. ANTECEDENTES
Se sabe que el carbono se presenta en formas y colores diversos, los más comunes son sólidos negros (coque, grafito) pero también se puede presentar como el cristalino y duro diamante. Además del carbón vegetal, en la naturaleza hay otras formas como la turba que es un material orgánico compacto, de color pardo oscuro y rico en carbono. Está formado por una masa esponjosa y ligera en la que aún se aprecian los componentes vegetales que la originaron. La formación de turba constituye la primera etapa del proceso mediante el cual la vegetación se transforma en carbón mineral. Se forma como resultado de la putrefacción y carbonificación parcial de la vegetación en el agua ácida de pantanos, marismas y humedales. La comprensión de la turba produce el lignito que ya es un carbón mineral en forma de sustancia desmenuzable, en la que aún se pueden reconocer algunas estructuras vegetales. Es de color negro o pardo y frecuentemente presenta una textura similar a la de la madera de la cual procede. La compresión del lignito originó la hulla, principalmente en la Era Primaria, durante los períodos Carbonífero y Pérmico. Surgió como resultado de la descomposición de la materia vegetal de los bosques primitivos, proceso que ha requerido millones de años. La hulla, 
figura 2, el tipo de carbón más abundante, es una roca sedimentaria orgánica, una clase de carbón mineral que contiene entre un 45 y un 85% de carbono. Es dura y quebradiza, estratificada, de color negro y brillo mate o graso.
Figura 2. La hulla. Fuente: http://www.laflecha.net/canales/ciencia/noticias/200607183 El coque es producto de la descomposición térmica de carbones bituminosos en ausencia de aire. Es un combustible logrado por destilación de la hulla a temperaturas muy altas en hornos cerrados y a la cual añaden calcita para mejorar su combustión, que la aíslan del aire, y que sólo contiene una pequeña fracción de las materias volátiles que forman parte de la misma.. Cuando la hulla se calienta desprende gases que son muy útiles industrialmente; el sólido resultante es el carbón de coque, que es liviano y poroso, figura 3.
Figura 3. El coque. Fuente: http://es.wikipedia.org/wiki/Archivo:Koks_Brennstoff.jpg El grafito es la forma alotrópica más estable del carbono. Está constituido por láminas planas de átomos de carbono que forman un sistema de anillos condensados. Las láminas están ordenadas en forma hexagonal y paralelas entre sí. Hay dos formas alotrópicas con diferentes secuencias de apilamiento: hexagonal y romboédrico. En cada lámina, cada átomo de carbono está unido a otros tres por medio de enlaces covalentes formando una serie continua de hexágonos. En el grafito hexagonal, la distancia entre los planos es de 0.3354, más del doble de la distancia del enlace C-C en los planos basales. Esto indica que la interacción entre láminas aromáticas es débil. Se asume que las láminas están unidas mediante enlaces de van der Waals e interacciones p-p, formando una red cristalina tridimensional. Debido a esto, el grafito posee un alto grado de anisotropía, de modo que sus propiedades eléctricas, térmicas y mecánicas varían notablemente dependiendo de la dirección en la cual se haga la medida.
El grafito natural comenzó a explotarse hacia 1564 cuando se descubrió la primera mena de este material desconocido por aquel entonces, por lo cual fue denominado plombagina, ya que presentaba un color gris parecido al del plomo y al igual que este dejaba marcas cuando se pasaba
por una superficie. El grafito sintético es un material constituido por carbón grafítico. Fue preparado por primera vez a principios del siglo XX, lo que contribuyó notablemente a ampliar el campo de aplicaciones del grafito, figura 4.
Figura 4. Grafito y su estructura. Fuente: http://carbono-fcc.blogspot.com/2009/03/grafito.html El diamante es la segunda forma alotrópica más estable del carbono, después del grafito; sin embargo y tiene renombre específicamente como un material con características físicas superlativas, muchas de las cuales derivan del fuerte enlace covalente entre sus átomos, figura 5.
Figura 5. Diamante y su estructura. Fuente: http://www.hull.ac.uk/chemistry/intro_inorganic/Diamond.htm La estructura de cada uno de estos materiales es lo que determina sus propiedades. Así los enlaces tridimensionales del diamante dan lugar a una estructura más robusta y por tanto a cristales más duros que en el caso del grafito, en el cual el enlace se limita a las dos dimensiones de las capas, que pueden deslizarse fácilmente entre sí, lo cual da lugar a un material blando que se usa como lubricante sólido.
Todo esto se sabe desde hace ya muchos años y así hasta el decenio de 1980 se conocían seis formas cristalinas del carbono: dos clases de grafito (el grafito hexagonal, que es la forma termodinámicamente estable en la que la secuencia de apilamiento de las láminas es ABAB; y el grafito romboédrico, que es una forma termodinámicamente inestable, y mucho menos abundante, con una secuencia de apilamiento ABCABC), dos clases de diamante (el diamante cúbico que es la estructura más habitual y el diamante hexagonal o lonsdaleita, figura 6, que se encontró por primera vez en 1967), la caoita o carbón blanco y el carbono (VI) que es similar
pero distinto a la caoita, estos dos últimos fueron descubiertos en 1968 y 1972 respectivamente. 1, 2, 3, 4, 5, 6
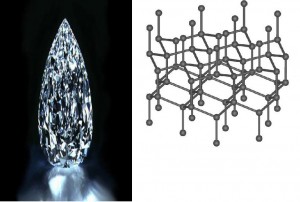Figura 6. La lonsdaleita y su estructura. Fuentes: http://science.kukuchew.com/2009/02/13/; http://www.cienciakanija.com/wp-content/uploads/lons.jpg.
3. LOS FULLERENOS
Sin embargo, a pesar de que el enlace del carbono ha sido uno de los más estudiados, en 1985 se descubrió una nueva forma del carbono (de hecho una familia entera de nuevas formas). El primer miembro de esta familia y el mejor conocido tiene una estructura esférica, compuesta por 60 átomos de carbono, como se muestra en la
figura 7. Esta bola, de fórmula C60, se conoce también como buckminsterfullereno o simplemente fullereno en honor del ingeniero norteamericano R. Buckminster Fuller, quien había diseñado una cúpula geodésica en la que usaban elementos hexagonales junto con alguno pentagonal para curvar la superficie. La molécula de fullereno es verdaderamente un asombroso conjunto de 60 átomos de carbono. Es la única molécula compuesta de un solo elemento que forma un esferoide hueco, que le da el potencial de llenarlo para múltiples aplicaciones.
Figura 7. El buckminsterfullereno Fuentes: http://www.abiertohastaelamanecer.ws/fp-content/images/fullenero.gif; http://guy.vielh.free.fr/mini_labo/footballene.jpg
Los científicos responsables del descubrimiento, por el que recibieron el Premio Nobel de Química en 1996, fueron los estadounidenses Robert F. Curl y Richard E. Smalley y el británico Harold W. Kroto. Los dos primeros, que trabajaban en la Universidad de Rice, lo hacían con una máquina de bombardeo y vaporización inventada por Smalley para conseguir racimos (clusters) de átomos metálicos. Usando rayos láser sobre barras de silicio las altas temperaturas obtenidas, de hasta diez mil grados, superiores a las existentes en las superficies de las estrellas, conseguían separar sus átomos convirtiéndolos en un plasma. Tras ello, en una cámara de vacío el plasma era sometido a una corriente de gas helio inerte y se obtenían unos racimos o agregados de átomos que eran estudiados mediante técnicas de espectrometría de masas. El británico Harold Kroto, de la Universidad de Sussex era un astroquímico que investigaba el origen del universo y de la materia viva, e intentaba hallar una explicación al polvo estelar. Concretamente trataba de conocer como se forman los agregados de carbono y nitrógeno (cianopolienos) que abundan en las atmósferas estelares. Kroto, conocedor de la máquina estadounidense, se trasladó a Houston y reemplazó el silicio por el carbono. Pronto comenzaron a acumularse resultados indicativos de que los átomos de carbono se disponían en una forma sorprendente y estable en agregados de 60 átomos de carbonos unidos entre sí. La unidad básica parecía ser una estructura de anillo hexagonal plano como el grafito, pero el aspecto global parecía ser esférico. De hecho lo que se descubrió no fue simplemente una nueva molécula sino una clase casi infinita de nuevas moléculas. Cada fullereno –C60, C70, C84, etc. – poseía la característica esencial de ser una cajita de carbono puro, con cada átomo enlazado a otros tres, como el grafito, pero a diferencia de éste, cada fullereno tiene exactamente 12 caras pentagonales con una cantidad variable de caras hexagonales (la bola Bucky tiene 20).p Desde entonces se han sintetizado fullerenos que tienen tamaños entre 24 y 540 átomos de carbono, amén de fullerenos de otros elementos. Las buckyballs de elementos distintos al carbono se han estudiado en el silicio, el nitruro de boro, el bisulfuro de molibdeno, BiS2, el oro, etc.7 En 1990 los físicos W. Krätschmer y D.R. Huffman por primera vez produjeron cantidades aislables de C60 con un arco entre dos barras de grafito, en una atmósfera de helio y extrayendo el condesado de carbono que se formaba por medio de un solvente. Desde que los fullerenos fueron producidos y purificados, han atraído el interés como un nuevo material promisorio con propiedades estructurales y electrónicas únicas. Tienen aplicaciones en nanoelectrónica porque sus propiedades electrónicas se pueden acondicionar con la adición de especies moleculares o elementales ya sea a la jaula del fullereno o dentro de ella. Un método importante de dopar es introducir átomos dentro de la jaula, produciendo un complejo exótico llamado fullereno endohédrico que varía las propiedades eléctricas y electrónicas, figura 8. El primero fue el LaC82, sin embargo, entre los más estudiados están los fullerenos dopados con metales alcalinos
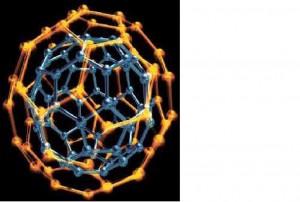Figura 8. Fullerenos endohédricos. Fuente: http://qsd.physics.ox.ac.uk/figs/nc60.png Los fullerenos han desarrollado un campo completamente nuevo en la química y la física de los materiales, con consecuencias en áreas tan diversas como la astroquímica, la ingeniería de materiales y la electrónica. Se usan en catalizadores, lubricantes y superconductores, sin embargo, al final de esta sección luego de revisar los nanotubos, se dará una reseña de aplicaciones de los fullerenos y los nanotubos. 8, 9, 10, 11, 12 Finalmente debe anotarse que hay fullerenos naturales, pues se han encontrado pequeñas cantidades de moléculas C60, C70, C76, y C84 en hollines formados por las descargas de los rayos en la atmósfera. Recientemente se encontraron fullerenos en una familia de minerales conocidos como shungitas en Carelia, Rusia.13
4. LOS NANOTUBOS DE CARBONO
Un nanotubo de carbono de pared sencilla (NTPS) se considera que está formado por el enrollamiento de una monocapa de grafito (llamada una capa de grafeno) para formar un cilindro sin costuras. Un nanotubo multipared (NTMP) se puede considerar, de una manera similar, como un ensamble coaxial de nanotubos de pared sencilla, como una mamá rusa, uno dentro de otro,figura 9; la separación entre las paredes es similar a la separación entre las capas del grafito natural. Por tanto los nanotubos son objetos unidimensionales con una dirección bien definida a lo largo del eje, que es similar a las direcciones en los planos del grafito. Sumio Iijima reportó la observación de los NTMPs en 199114 y luego, en 1993, dos grupos independientes, Iijima e Ichihashi15 y Bethune et al16 reportaron el crecimiento de NTPSs en la misma entrega de Nature. El impacto de estas cartas a la revista fue tremendo entre los científicos de materiales, y ello tal vez dio real inicio a la nanociencia y la nanotecnología. Sin embargo, la primera observación de los NTMPs se registró en 1952 en una publicación de Radushkevich y Lykianovic hecha en la Revista Soviética de Fisicoquímica17 y una imagen de un NTMP fue publicada por Oberlin et al. en la Revista de Crecimiento Cristalino.18 Así pues los nanotubos de carbón son grandes macromoléculas que son únicas por su tamaño, forma y notables propiedades físicas, independientemente de quien los descubriera.
a. b.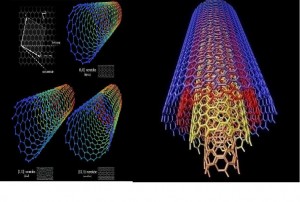 
Figura 9. a. Tipos de nanotubos monopared; b. nanotubo multipared. Fuentes: http://simplechemconcepts.com/wp-content/uploads/2008/03/carbon_nanotubes.png; http://students.chem.tue.nl/ifp03/images/mwnt.gif Esas intrigantes estructuras han despertado mucho interés y se hace mucha investigación al respecto. Las propiedades físicas se continúan descubriendo, pero es difícil porque los nanotubos tienen un amplio intervalo de propiedades electrónicas, térmicas y estructurales que cambian con los diferentes tipos de nanotubos (definidos por su diámetro, longitud y quiralidad o ángulo de torsión).19, 20 Los nanotubos multipared se han usado en matrices poliméricas o en sistemas metálicos para producir materiales más tenaces, fuertes y livianos. Productos que se pueden usar en aspas de rotores para turbinas de viento, contenedores para el transporte o equipos deportivos. El hecho es, entonces que la estructura, fabricación y propiedades de fullerenos y nanotubos se continúan investigando febrilmente en catálisis, superconductividad, electrónica y materiales reforzados. Como es la única molécula esférica, la bola de Bucky puede soportar que se le golpee contra una placa de acero inoxidable a 24 000 kmph, rebotando sin ningún problema. Cuando se comprime al 70% de su tamaño original, se hace dos veces más duro que el diamante.21 Los fullerenos son resistentes al calor y (únicos entre los alotropos del carbono) se disuelven en los solventes comunes a temperatura ambiente. Tiene aplicaciones como superconductores, catalizadores para mejora de los hidrocarburos y como fármacos, porque el C60 es altamente hidrofóbico y antioxidante, envuelven a los radicales libre que dañan las células. Como refuerzos posiblemente sirvan para hacer materiales superresistentes y nanoalambres. Además sirven como aditivos de los polímeros para crear nuevos copolímeros con propiedades específicas.
El C60 sirve para catálisis de oxigenación de los materiales orgánicos y así puede purificar el agua y proteger contra los peligros biológicos. Son promisorios para las membranas de intercambio de protones en las celdas de combustible y para el almacenamiento de hidrógeno.22, 23 Para las puntas de los microscopios de barrido con sonda, como los de fuerza atómica y efecto túnel, los nanotubos son ideales por su pequeño diámetro y alta relación de esbeltez. Los fullerenos y sus derivados también se usan para recubrimientos de ciertos sensores como la microbalanza de cuarzo y los sensores superficiales de onda acústica. También se han desarrollado sensores moleculares basados en nanotubos monopared semiconductores. Así mismo se usan como fuentes de emisión de campo. En general, las aplicaciones de fullerenos y nanotubos se siguen desarrollando.24, 25, 26
5. HISTORIA DEL GRAFENO
Los fullerenos y los nanotubos están constituidos por capas de átomos de carbono, llamadas grafeno, o sea que éste se conocía desde hace años, pero apenas en el año 2004 fue aislado, en la Universidad de Mánchester, como bien lo comunicó el grupo de materia condensada: “We found a new class of materials which is now referred to as 2D atomic crystals. Such crystals can be seen as individual atomic planes “pulled out” of bulk, 3D crystals. Despite being only one atom thick and unprotected from the immediate environment, these materials are stable under ambient conditions, exhibit high crystal quality and are continuous on a macroscopic scale.”27 El término grafeno se usó por primera vez en 1987 para describir láminas singulares de grafito usadas como constituyentes de los compuestos de intercalación de grafito (CIGs); conceptualmente un CIG es una sal cristalina de un intercalante y un grafeno, figura 10.28 Como ya se ha señalado, el término también se usó en las descripciones iniciales de los nanotubos de carbono,29 así como para explicar el grafeno epitaxial,30 y los hidrocarburos aromáticos policíclicos.31 En principio no se podían producir moléculas o láminas mayores de grafeno (de modo que se pudieran considerar verdaderos cristales bidimensionales aislados). Un artículo en Physics Today decía: “Fundamental forces place seemingly insurmountable barriers in the way of creating [2D crystals]… The nascent 2D crystallites try to minimize their surface energy and inevitably morph into one of the rich variety of stable 3D structures that occur in soot. But there is a way around the problem. Interactions with 3D structures stabilize 2D crystals during growth. So one can make 2D crystals sandwiched between or placed on πgraphite… One can then hope to fool Nature and extract single-atom-thick crystallites at a low enough temperature that they remain in the quenched state prescribed by the original higher-temperature 3D growth.”32
Figura 10. Compuesto de intercalación de grafito (CIG). Fuente: http://cp2s.uhp-nancy.fr/php/205_E?PHPSESSID=eac1e2b7619ce20ac25cd63c00c8de2f Desde el decenio de 1970 se empezaron a crecer epitaxialmente monocapas de grafito encima de otros materiales.33 Este “grafeno epitaxial” estaba constituido por una monocapa de átomos de carbono en una reda hexagonal unida por enlaces sp2, como en el grafeno libre. Sin embargo, hay una transferencia significativa de carga desde el grafeno epitaxial hacia el sustrato, y, en algunos casos, hibridación entre los orbitales de del sustrato y los orbitales π del grafeno, la cual altera significativamente la estructura electrónica del grafeno epitaxial. Las monocapas de grafito también se observaron por TEM en materiales volumétricos, en particular en hollín obtenido por exfoliación química. También se hicieron muchos esfuerzos para lograr películas muy delgadas desde el decenio de 1990 hasta 2004, pero el mínimo espesor alcanzado fue de 50 capas.34 El avance clave en la tecnología del grafeno ocurrió cuando Andre Geim y Kosntantyn Novoselov, en el Instituto de Materia Condensada de la Universidad de Mánchester, Inglaterra lograron extraer del grafito cristales con el espesor de una monocapa.35 Como le contó Novosolev a Dan Vergano: “Habíamos estado ensayando varios métodos en nuestro laboratorio y un investigador estaba preparando muestras volumétricas de grafito para las pruebas. La manera de limpiar el grafito es cubrirlo con cinta pegante, arrancar la cinta y botarla. De modo que alguna vez, recogí una cinta de esas de la basura y la analicé”36, así se obtuvo el grafeno, figura 11. Las capas de grafeno que se encontraron en la cinta las transfirieron sobre una oblea de sílice con una técnica llamada clivaje micromecánico o, simplemente, la técnica de la cinta pegante. La sílice aisló eléctricamente el grafeno, porque interactúa débilmente con él, de modo que se obtuvieron capas casi neutras eléctricamente. La sílice debajo del grafeno se puede usar como un electrodo de “puerta trasera” para variar, en un amplio intervalo, la densidad de la carga en la capa de grafeno.
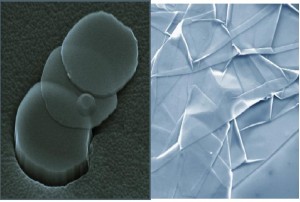Figura 11. Despegando repetidamente capas cada vez más delgadas con la cinta pegante,
(izquierda), se obtuvieron monocapas (derecha) como se ve en estas fotos SEM.
Fuente: http://physics.bu.edu/documents/pw1106.pdf
Esta técnica permitió la primera observación del efecto Hall cuántico anómalo en el grafeno37, 38
lo cual proporcionó evidencia directa de lo predicho por Berry, de que había una fase π de
fermiones sin masa en el grafeno. Hay dos tipos de efecto Hall cuántico entero. Uno es
característico de los sistemas semiconductores bidimensionales, y el otro es la contraparte
relativística observada en el grafeno, donde los portadores de carga imitan a los fermiones de
Dirac caracterizados por la fase π de Berry, lo cual proporciona otro tipo de respuesta en el
material.
El efecto Hall cuántico anómalo hace que la conductividad perpendicular a la corriente tome
valores discretos, o cuantizados, lo que permite medirla con una precisión increíble. La
cuantización implica que la conductividad del grafeno nunca puede ser cero (su valor mínimo
depende de la constante de Planck y la carga del electrón).
Ya se anotó que los electrones que se mueven en el grafeno se comportan como cuasipartículas
sin masa, que son los llamados fermiones de Dirac. Dichos fermiones se mueven a una velocidad
constante independientemente de su energía (como ocurre con la luz), en este caso a unos
106 m/s. La importancia del grafeno, en este aspecto, consiste en que permitió comprobar
experimentalmente este comportamiento que había sido predicho teóricamente hace más de 50
años.
Es decir, que el efecto Hall cuántico permite que los electrones actúen juntos para crear unas
nuevas partículas virtuales con cargas eléctricas que son una fracción de la carga del electrón.
Debido a las propiedades anteriores, los electrones del grafeno pueden moverse libremente por
toda la lámina y no quedarse aislados en zonas de las que no pueden salir (efecto llamado
localización de Anderson, y que es un problema para sistemas bidimensionales con impurezas).
Es casi completamente transparente y tan denso que ni siquiera el átomo de helio, cuyos átomos
son los más pequeños que existen (sin combinar en estado gaseoso) puede atravesarlo.
El efecto Hall cuántico anómalo fue reportado casi al mismo tiempo por Geim y Novoselov39 y por Philip Kim y Yuanbo Zang.40 Las investigaciones sobre el grafeno, su estructura y propiedades son cada vez más complejas y abundantes.41
6. CARACTERÍSTICAS DEL GRAFENO
Es conveniente dejar claro qué es un cristal bidimensional; obviamente un plano monoatómico es un cristal 2D, mientras que 100 monocapas se deben considerar como una película delgada de un material tridimensional. ¿Pero cuántas capas se necesitan para hacer una estructura 3D? Para el grafeno la situación se ha hecho clara pues la estructura electrónica evoluciona rápidamente con el número de capas y se aproxima al límite tridimensional con unas diez.42 Más aún, sólo el grafeno y su bicapa tienen espectros electrones sencillos: son semiconductores con laguna cero (o semimetales con cero solape) con un tipo de electrones y un tipo de huecos. Para 3 o más capas, los espectros se van volviendo más complicados, es decir aparecen varios portadores43, y las bandas de conducción y de valencia empiezan a solaparse. Esto permite distinguir entre las monocapas, las bicapas y unas pocas capas (3 a 10) como tres tipos de grafeno. Las estructuras más gruesas se pueden considerar, para todos los propósitos como, películas delgadas de grafito. Puede entenderse que el grafeno es la unidad fundamental de todas las formas de grafito, figura 12.
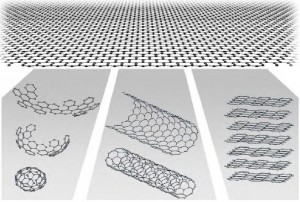Figura 12. Madre de todas las formas de grafito. El grafeno es el material de construcción bidimensional para los materiales carbonáceos de todas las otras dimensiones. Se puede curvar en fullerenos 0D, enrollar en nanotubos 1D y apilarse en grafito 3D. Fuente: Geim, A. K. and K. S. Novoselov, “The raise of Graphene”, Nature materials, Vol. 6, March 2007, p. 183.
Los cristales bidimensionales no sólo son continuos sino que exhiben una elevada cristalinidad.44 – 49 Esto último es más evidente para el grafeno, en el cual los portadores de carga pueden viajar miles de distancias interatómicas sin dispersarse. Con el beneficio, en retrospectiva, de que la existencia de tales cristales monocapa se puede reconciliar con la teoría. En realidad se puede argumentar que estos cristales 2D están congelados en el estado metaestable porque se extraen de materiales tridimensionales, en tanto que su pequeño tamaño (<<< 1 mm) y los fuertes enlaces interatómicos aseguran que las fluctuaciones térmicas no llevarán a la generación de dislocaciones u otros defectos incluso a temperaturas elevadas.50, 51 En cuanto a su conductividad eléctrica, esta puede entenderse de manera sencilla si se visualiza que tiene un electrón común que queda libre cuando cada átomo de carbono se enlaza con otros tres, haciéndolo así un excelente conductor, figura 13.52 Esta hibridación sp2 forma un enlace fuerte y direccional que determina la estructura en forma de colmena y explica también la fortaleza del material, figura 14.53 Debido a esta características es que el grafeno posee alta conductividad térmica y eléctrica54, 55; elevada elasticidad y dureza56; resistencia mecánica que es 200 veces mayor que la del acero; puede reaccionar químicamente con otras sustancias para formar compuestos con diferentes propiedades, lo que dota a este material de gran potencial de desarrollo; soporta la radiación ionizante; es muy ligero, como la fibra de carbono, pero más flexible; tiene menor efecto Joule, es decir, se calienta menos al conducir los electrones; consume menos electricidad para una misma tarea que el silicio.
Figura 13. Si se cambia la configuración de los orbitales electrónicos en los átomos de carbono se producen formas muy diferentes de carbono puro. En el diamante (derecha), todos los cuatro electrones de valencia están involucrados en el fuertes enlace σ (hibridación sp3). El ángulo entre los enlaces es aproximadamente de 109º, y de aquí las formas tridimensionales. Para los átomos de grafeno, solamente tres electrones forman enlaces σ (hibridación sp2), y esos enlaces están en un plano a 120º entre sí, produciendo una estructura plana. El cuarto electrón es común, forma
enlaces más débiles y hace del grafeno un excelente conductor. Las nubes azules son enlaces σ y las púrpura con enlaces π. Fuente: Novoselov, Konstantin, “Beyond de wonder material”, Physics World, August 2009, p. 27 Es decir que, como se esquematiza en la figura 13, los cuartos electrones no enlazados están en orbitales π que se extienden verticalmente por encima y por debajo del plano, y la hibridación de ellos se extiende sobre toda la lámina de grafeno. Así, esos enlaces π son los responsables de la conductividad del grafeno, figura 15.
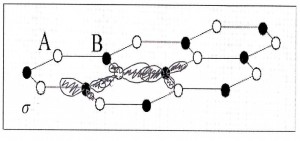Figura 14. Los enlaces σ explican la gran resistencia del grafeno. Fuente: http://www.lancs.ac.uk/users/esqn/phys421/Nano-Graphene-Nanotubes.pdf
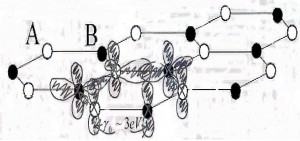Figura 15. Los enlaces π explican la conductividad del grafeno. Fuente: http://www.lancs.ac.uk/users/esqn/phys421/Nano-Graphene-Nanotubes.pdf El resumen de estas características está en la figura 16.
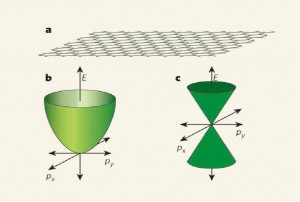Figura 16. a. La red en forma de colmena explica la Resistencia y la buena conductividad. Cada átomo de carbono (punto verde) usa tres de sus electrones de valencia para formar fuertes enlaces covalentes, dejando uno que queda disponible para la conducción. b. La relación cuadrática newtoniana entre la energía y el momento (E = p2/2m*) es obedecida por los electrones en un semiconductor. c. La relación energía – momento es muy diferente para los electrones del grafeno E = v|p|, lo que permite que se modelen como partículas sin masa y relativísticas, de acuerdo con la formulación de Dirac de la Mecánica Cuántica. Fuente: http://www.nature.com/materials/news/news/051110/438168a_f1.html En la figura 17 se visualiza lo mismo, pero es más clara la estructura de bandas del grafeno. Esa estructura se visualiza también en la figura 18.
a. b. c.
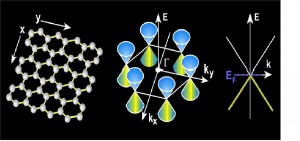Figura 17. a. Red del grafeno; b. Estructura de bandas del grafeno. Las bandas de valencia y conducción se tocan en los extremos de la primera zona de Brillouin y tienen forma de conos; c. La dispersión lineal tiene consecuencias profundas. Los electrones y huecos no se pueden describir con la ecuación de Schödinger; más bien son fermiones sin masa de Dirac con una velocidad efectiva de 1/300 de la velocidad de la luz. Fuente: http://www.fkf.mpg.de/klitzing/research_topics/research_topics_details.php?topic=Graphene
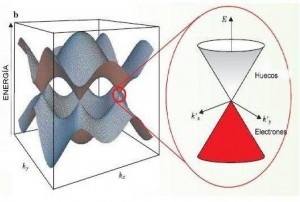Figura 18. Estructura de las bandas electrónicas del grafeno. Fuente: http://www.lps.u-psud.fr/spip.php?article462&lang=en En resumen, la estructura del grafeno es como se ve en la figura 19, el arreglo cristalino consiste en un ordenamiento hexagonal bidimensional, en tanto que su estructura de bandas está constituida por dos bandas (amarilla) que se interceptan sólo en unos pocos puntos de las esquinas de una zona hexagonal de Brillouin (rojas).
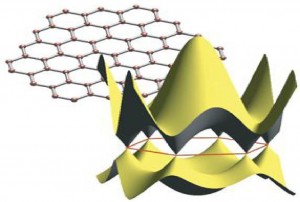Figura 19. Estructura cristalina y de bandas del grafeno Fuente: http://www.als.lbl.gov/als/science/sci_archive/154graphene.html
7. PROPIEDADES MECÁNICAS DEL GRAFENO
Las propiedades mecánicas del grafeno han sido determinadas por diferentes métodos, como el abombamiento de membranas, la nanoindetación, el oscilador armónico, las vigas doblemente empotradas o en voladizo, dinámica de membranas, dinámica de placas, actuadores vibrantes, detección óptica, deflexión de vigas, aplicación de sistemas microelectromecánicos y sistemas nanoelectromecánicos. 57, 58, 59 El grafeno tiene una resistencia a la cedencia de 130 GPa, un módulo de elasticidad de 1.06 TPa, y una relación de Poisson de ν = 0.186, sin embargo, a pesar de esa elevada rigidez, las láminas de grafeno tienen una gran flexibilidad, lo cual se atribuye al cambio en la curvatura dado por el alargamiento reversible de los enlaces sp2.60, 61, 62 Además, debido a la baja densidad de defectos en las películas, el comportamiento elástico del grafeno refleja las propiedades intrínsecas del enlace interatómico en toda su resistencia hasta el punto de ruptura. Por consiguiente, la respuesta del grafeno se debe considerar no lineal pues la gráfica tensión – deformación se debe curvar sobre el punto máximo que indica la tensión de ruptura. De esa manera el comportamiento elástico surge del término del menor orden, cuadrático, en la energía potencial, en tanto que el término de tercer orden origina el comportamiento no lineal.63 En el modelo más sencillo, la respuesta elástica isotrópica bajo tensión uniaxial se puede expresar como σ = Eε + Dε2 donde σ es la tension, ε la deformación unitaria, E el módulo de Young y D el módulo elástico de tercer orden. Normalmente el valor de D es negativo (-2 TPa) , de modo que la presencia del término de segundo orden lleva una disminución de la rigidez para deformaciones de tracción elevadas y una respuesta cada vez más rígida para deformaciones elevadas de compresión. Las simulaciones numéricas de las láminas de grafeno y de nanotubos sugieren que esta respuesta no lineal es adecuada para describir el material.64, 65, 66, 67
8. PROPIEDADES ELECTRÓNICAS
Como se ha repetido, uno de los aspectos más interesantes del grafeno es que sus excitaciones de baja energía son fermiones de Dirac, sólo que estos se mueven a una velocidad menor que la predicha por la electrodinámica cuántica (EDC), pues vF es 300 menor que la velocidad de la luz c. Por ello muchas de las propiedades inusuales de la EDC aparecen en el grafeno pero a menores velocidades. Los fermiones de Dirac se comportan de manera extraña si se comparan con los electrones ordinarios en los campos magnéticos, lo cual da como resultado nuevos fenómenos físicos como el anómalo efecto Hall cuántico entero (EHCE) que además de ser diferente al EHCE exhibido por el silicio y en el arseniuro de galio y aluminio, se puede observar a temperatura ambiente. .En efecto, el EHCE es la marca de fábrica del comportamiento de los fermiones de Dirac.
Otra característica interesante de los fermiones de Dirac es su insensibilidad a los potenciales electrostáticos externos debido a la llamada paradoja de Klein, esto es el hecho de que los fermiones de Dirac se pueden transmitir con una probabilidad de 1 en una región prohibida clásicamente. Por ello los fermiones de Dirac se comportan distinto en la presencia de potenciales de confinación, lo que genera el fenómeno de Zitterbewegung, o movimiento saltón (nervioso) de la función de onda Itzykson, C., and J.-B. Zuber, 2006En el grafeno esos potenciales electrostáticos pueden ser generados fácilmente por el desorden. Y como el desorden es inevitable en cualquier material, ha habido mucho interés en entender cómo el desorden afecta la física de los electrones en el grafeno y sus propiedades de transporte. De hecho, y como ya se mencionó, bajo ciertas condiciones, los fermiones de Dirac son inmunes a los efectos de localización observados en los electrones ordinarios y se ha establecido que tales electrones se pueden propagar sin dispersarse sobre distancias del orden de los micrómetros. .Las fuentes de desorden en el grafeno son muchas y pueden variar desde los efectos comunes encontrados en los semiconductores, como las impurezas ionizadas en el sustrato de Si, a átomos adsorbidos y varias moléculas adsorbidas en la superficie del grafeno, hasta efectos menos usuales como las ondulaciones asociadas con la estructura blanda del grafeno. De hecho el grafeno es único en el sentido de que comparte las propiedades de las membranas blandas y al mismo tiempo se comporta de una manera metálica, de modo que los fermiones se propagan en un espacio curvado localmente. La blandura del grafeno se relaciona con los modos vibracionales fuera del plano, fonones que no se pueden encontrar en los sólidos tridimensionales. Estos modos flexurales, que son los responsables de las propiedades flexibles del grafeno, también contribuyen a la falta de orden estructural de largo alcance en las membranas delgadas, lo que produce el fenómeno de abollamiento o arrugamiento. .A pesar de ello, la presencia de un andamio o sustrato que mantiene el grafeno en su lugar puede estabilizarlo hasta cierto grado pero deja tras de si los rizos que se pueden visualizar como nodos de flexión congelados También se ha notado que el grafeno puede presentar efectos mesoscópicos. Esos efectos tienen su origen en las condiciones límites requeridas por las funciones de onda en las muestras mesoscópicas con varios tipos de bordes, que puede tener el grafeno. Los bordes más estudiados, en zigzag y en forma de brazo de silla, tienen propiedades electrónicas muy diferentes. La naturaleza de Dirac de los fermiones del grafeno se puede usar para controlar en sabor en el valle de los electrones, además de su carga, la llamada valletrónica. .Más aún, cuando se unen contactos superconductores al grafeno, se desarrolla un flujo de supercorriente y un proceso de Andrew, característico de la proximidad del efecto superconductor. .El hecho de que los pares de Cooper se puedan propagar tan bien en el grafeno da testimonio de la robusta coherencia electrónica del material. Además se han observado experimentalmente fenómenos como la localización débil, las fluctuaciones universales de conductancia, y el efecto Aharonov-Bohm. 68, 69, 70
9. APLICACIONES
Las asombrosas propiedades de transporte del grafeno ya mencionadas han hecho pensar que el grafeno puede, eventualmente, suplantar al silicio en los chips de computador, con la perspectiva de aparatos ultrarrápidos operando a velocidades de Terahertz. Sin embargo, de acuerdo con los expertos, los microprocesadores de grafenium se demoran por lo menos 20 años. Entre tanto se espera que maduren otras muchas aplicaciones del grafeno. El uso más inmediato puede ser en materiales compuestos pues se ha demostrado que el polvo de grafeno se puede producir en masa, lo que permitiría desarrollar plásticos conductores con rellenos de menos de 1 % en volumen. Otra posibilidad atractiva es el uso de polvo de grafeno en las baterías eléctricas que son en la actualidad el principal mercado para el grafito. Una mejor relación superficie/volumen y la elevada conductividad pueden mejorar la eficiencia de las pilas reemplazando las nanofibras de carbono que se usan en las baterías modernas. Las aplicaciones más nuevas del grafeno se relacionan con su transparencia y su alta conductividad para su uso para electrodos en pantallas planas y celdas solares. Actualmente, por su transparencia, el óxido de indio es el material usado en tales electrodos, pero presenta el problema de que es muy escaso en el planeta, por tanto las investigaciones buscan nuevos materiales con excelentes propiedades conductivas y que puedan ser aplicados en optoelectrónica. Precisamente, investigadores del instituto Max Planck en Mainz, Alemania han demostrado que las películas delgadas de grafeno son una buena opción para ser usados como electrodos pues tienen alta conductividad, buena transparencia en ambas regiones de infrarrojo y visible, una superficie ultrasuave y es química y térmicamente estable. Además el equipo preparó celdas solares orgánicas con una película delgada de grafeno con cuarzo como ánodo. Las hojas de grafeno trabajan de forma óptima, aunque existe la posibilidad de mejorar las propiedades del mismo al incrementar la conductividad de la película de grafeno. Los investigadores creen que los electrodos transparentes de grafeno se pueden aplicar en diodos emisores de luz orgánicos, en pantallas planas y otros dispositivos optoelectrónicos. Finalmente, no puede dejar de mencionarse el almacenamiento de hidrógeno, que ha sido un tema muy activo y controvertido con los nanotubos. Se ha sugerido que el grafeno es capaz de absorber una gran cantidad de hidrógeno y se esperan muchos esfuerzos experimentales en esta dirección.
Debido a su especial flexibilidad estructural y electrónica el grafeno se puede moldear química y estructuralmente de diferentes manera: deposición de átomos o moléculas encima; intercalación como en los compuestos de intercalación en grafito; incorporación de nitrógeno y boro en su estructura, en analogía con lo que se ha hecho con los nanotubos y usando diferentes sustancias que modifican la estructura electrónica.71
El control de las propiedades del grafeno se puede extender en nuevas direcciones permitiendo la creación de sistemas basados en él con propiedades magnéticas y superconductoras, que son únicas en dos dimensiones.72 Todas estas propiedades hacen que el grafeno sea una alternativa como conductor transparente, de los que ahora se utilizan en todas partes, desde los monitores de computadores y pantallas de televisión hasta las pantallas táctiles y las celdas solares. Pero el material ha sido difícil de fabricar en tamaños superiores a unos cuantos centímetros cuadrados. Ahora los investigadores han creado láminas de grafeno rectangulares de 76 cm de diagonal y las han usado para crear pantallas táctiles que funcionan. En efecto, el año pasado un grupo de la Universidad de Texas, en Austin, liderado por Rodney Ruoff, creció cuadrados de grafeno, de 1 cm, sobre láminas flexibles de cobre.73 Luego los investigadores Jong-Hyun Ahn y Byung Hee Hong de la Universidad Sungkyunkwan, en Corea del sur, escalaron el trabajo de los texanos e hicieron láminas lo suficientemente grandes como para hacer pantallas. Para ello utilizaron CVD y depositaron grafeno sobre grandes láminas de cobre. Luego añadieron un adhesivo sobre el grafeno y disolvieron el cobre. Al despegar el adhesivo obtuvieron una monocapa de grafeno, figura 20; para fortalecerla apilaron cuatro monocapas y las trataron químicamente con ácido nítrico para mejorar su conductividad eléctrica.
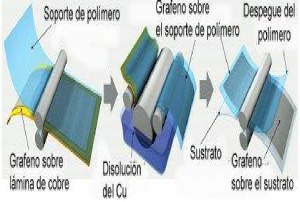Figura 20. Obtención de grandes laminas de grafeno. Fuente: http://news.sciencemag.org/sciencenow/2010/06/graphene-finally-goes-big.html La película permite el paso del 90% de la luz y tiene una resistencia eléctrica menor que la del conductor corriente que es de óxido de indio y estaño. Los miembros del grupo también revelaron que el grafeno funcionó mejor que el óxido en una pantalla, el cual además es frágil, mientras que la pantalla de grafeno soporta el doble de deformación que los aparatos convencionales basados en el óxido.74 Papel de óxido de grafeno Por último es conveniente añadir que papel de óxido de grafeno u óxido de papel de grafito es un material compuesto fabricado con óxido de grafito. El material tiene rigidez y resistencia excepcionales, debido a la resistencia intrínseca de la red de grafeno y su estructura bidimensional que distribuye las cargas. El material de inicio son escamas de óxido de grafeno dispersadas en agua, las cuales se pueden unir químicamente para desarrollar un material nuevo. El papel de óxido de grafeno es aislante eléctrico, pero sus propiedades se pueden modular para hacerlo conductor o semiconductor sin perder propiedades mecánicas.75
Se pensaba que este material es hidrofílico, pero los estudios han mostrado que tiene regiones hidrofóbicas o sea que el material en general es anfifílico. Todas estas propiedades hacen que el papel de óxido de grafeno se pueda aplicar en memorias de computador, aparatos optoelectrónicos, baterías, supercondensadores, membranas porosas y para fabricar materiales compuestos con polímeros, cerámicas y metales.
10. CONCLUSIÓN
Como se ha resumido el grafeno y el óxido de grafeno son materiales que están en pleno desarrollo y sus aplicaciones tecnológicas apenas empiezan. Se vislumbran muchas posibilidades y no es de extrañar que a quienes lo aislaron les hayan dado el premio Nobel. Aunque es preciso anotar que en la actualidad hay también otra serie de materiales que están siendo investigados y desarrollados.76 En fin, la intención de reseñar estos materiales es hacer que nuestros estudiantes e investigadores se aproximen a ellos y los tengan en cuenta en sus proyectos.
11. REFERENCIAS BIBLIOGRÁFICAS
1. Tascón, Juan M. D., “Materiales de carbono: estructuras y formas”, Óptica pura y aplicada, Vol. 40, No 2, 2007, p. 149.
2. Whittaker, A. Greenville and Gerard M. Wolten, “Carbon: A Suggested New Hexagonal Crystal Form”, Science 6, October 1972, Vol. 178. No. 4056, p. 54.
3. Fitzer, E., K. H. Köchling, H. P. Boehm, H., Marsh, “Recommended terminology for the description of carbon as a solid (IUPAC Recommendations 1995)”, Pure Appl. Chem., Vol. 67, 1995, p. 473.
4. Rodríguez-Reinoso, F., “Comité internacional para la caracterización y la terminología del carbón”, Carbon, Vol. 27, 1989, p. 305.
5. Edwards, I . A. S. “Structure in carbons and carbon forms”, Introduction to Carbon Science (H.Marsh Ed.), Butterworths, London, 1989, p. 1.
6. Marsh, H., “Carbon materials: an overview of carbon artefacts”, Introduction to Carbon Technologies, H. Marsh, E. A. Heintz y F. Rodríguez-Reinoso, Eds., Servicio de Publicaciones de la Universidad de Alicante, Alicante, 1997, Cap. 1.
7. Natalia Dubrovinskaia et al “Superhard nanocomposite of dense polymorphs of boron nitride: Noncarbon material has reach diamond hardness.” Appl. Phys. Lett. Vol. 90, 2007, p. 91.
8. Smalley, Richard E. and Boris I. Yakobson, “The future of the fullerenes”, Solid State Communications, Vol. 107, No. 11, 1998, p. 597.
9. Martín León, Nazario, “Los fullerenos: moléculas de carbono con propiedades excepcionales”, Anales de la Sociedad Española de Química, Segunda época Enero –Marzo, 1999, p. 14.
10. Mattesini, M. et al, “Electronic structure and optical properties of solid C60”, Physica B, Vol. 404, 2009, p. 1776.
11. Baldwin, J., Buckyworks, John Wiley, New York, 1996, p. 56.
12. Cavieres, Andrés, “Buckyballs”, Nanotecnología, http://www.euroresidentes.com/futuro/nanotecnologia/diccionario/Buckyballs.htm
13. “The allotropes of carbon”, http://invsee.asu.edu/nmodules/Carbonmod/everywhere.html
14. Iishima, Sumio, “Helical microtubules of graphitic carbon”, Nature, Vol. 354, 1991, p. 56.
15. Iijima, Sumui and Toshinari Ichihasshi, “Single-Shell carbon nanotubes of 1 nm diameter”, Nature, Vol. 363, 1993, p. 603.
16. Bethune, D. S. et al, “Cobalt catalyzed growth of carbon nanotubes with single atomic layer walls, Nature, Vol. 363, p. 605.
17. Radushkevich L. V., Lukyanovich V. M., “O strukture ugleroda, obrazujucegosja pri termiceskom razlozenii okisi ugleroda na zeleznom kontakte”, Zurn Fisic Chim, Vol. 26, 1952, p. 88.
18. Oberlin, A., M. Endo and T. Koyama, “Filamentous growth of carbon through benzene decomposition”, J. Crystl Growth, Vol 32, 1976, p. 335.
19. Ruoff, Rodney S. and Donald C. Lorents, “Mechanical and thermal properties of carbon nanotubes”, Carbon, Vol. 33, No. 7, 1995, p. 225.
20. Kuzmany, H., “Vibrational spectra of single wall carbon nanotubes”, Carbon, Vol. 36, No 5, 1998, p. 709.
21. Segawa, Craig, “The Buckyball: An Excruciatingly Research Report”, Honolulu Community College, http://www.insite.com.br/rodrigo/bucky/buckyball.txt.
22. Simonyan. Vahan V. and J. Karl Johnson, “Hydrogen storage in carbon nanotubes and graphitic nanofibers”, Journal of Alloys and Compounds, Vol. 330-332, 202, p. 659.
23. Cheng, Hui Ming, Quang Hong Yang and Chang Liu, “Hydrogen storage in carbon nanotubes”, Carbon, Vol. 39, 2001, p. 1447.
24. Jian, Tang, “The Discovery and Applications of Fullerenes”, Literature Seminar, The University of Alabama, October 4, 2005.
25. Iijima, Sumio, “Carbon nanotubes: Past. Present and Future”, Physica B, Vol. 323, 2002, p. 1.
26. Dai, Hongjie, “Nanotubes: opportunities and challenges”, Surface Science, Vol. 500, 2002, p. 218.
27. Condensed Matter Physics Group, “Graphene and Other Two-Dimensional Materials”, http://www.condmat.physics.manchester.ac.uk/research/graphene/
28. Mouras, S. et al. «Synthesis of first stage graphite intercalation compounds with fluorides». Revue de Chimie Minerale, Vol. 24, 1987,. p. 572.
29. Saito, R. et al. «Electronic structure of graphene tubules based on C60». Phys. Rev. B, Vol. 46, 1992, p. 1804.
30. Forbeaux, I. et al. «Heteroepitaxial graphite on 6H-SiC(0001): Interface formation through conduction-band electronic structure». Phys. Rev. B, Vol. 58, 1998, p. 16396.
31. Forbeaux, I. et al. «Heteroepitaxial graphite on 6H-SiC(0001): Interface formation through conduction-band electronic structure». Phys. Rev. B, Vol. 58, (1998), p. 16396.
32. Geim, A. K. & MacDonald, A. H., «Graphene: Exploring carbon flatland». Physics Today, Vol. 60, 2007, p. 35.
33. Oshima, C. and Nagashima, A., «Ultra-thin epitaxial films of graphite and hexagonal boron nitride on solid surfaces». J. Phys.: Condens. Matter, Vol. 9, 1997, p. 1.
34. Geim, Andre K. and Philip Kim, “Carbon Wonderland”, Scientific American, April 2008, p. 8.
35. Novoselov, K. S. et al. «Electric Field Effect in Atomically Thin Carbon Films». Science, Vol. 306, 2004, p 5696.
36. Vergano, Dan “Physics: Nobel Prize discovery was fished from the trash”; http://content.usatoday.com/communities/sciencefair/post/2010/10/2010-physis-nobel-prize-reaction-round-up/1
37. Novoselov, K. S. et al. «Two-dimensional gas of massless Dirac fermions in graphene». Nature, Vol. 438, 2005, p. 197.
38. Zhang, Y., Tan, Y. W., Stormer, H. L., and Kim, P. «Experimental observation of the quantum Hall effect and Berry’s phase in graphene». Nature, Vol. 438, 2005, p. 201.
39. Novosolev, K. S. et al, “Unconventional quantum Hall effect and Berry’s phase of 2π in bilayer graphene”, Nature Physics, No. 2, 2006, p. 177.
40. Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; and Kim, P. «Experimental observation of the quantum Hall effect and Berry’s phase in graphene». Nature, Vol. 438, 2005, p. 201.
41. “Graphene”, http://en.wikipedia.org/wiki/Graphene
42. Partoens, B. and Peeters, F.M. “From graphene to graphite: Electronic structure around the K point”. Phys. Rev. B, Vol. 74, 2006.
43. Morozov, S.V. et al. Two-dimensional electron and hole gases at the surface of graphite. Phys. Rev. B, Vol. 72, 2005, 201401
44. Novoselov, K. S. et al. “Electric field effect in atomically thin carbon films”. Science, Vol. 306, 2004, p. 666.
45. Novoselov, K. S. et al. “Two-dimensional atomic crystals”. Proc. Natl Acad. Sci. USA, Vol. 102, 2005, p.10451
46. Novoselov, K. S. et al. “Two-dimensional gas of massless Dirac fermions in graphene”. Nature, Vol. 438, 2005, p.197.
47. Zhang, Y. et al, “Experimental observation of the quantum Hall effect and Berry’s phase in graphene”. Nature, Vol. 438, 2005, p. 201.
48. Stankovich, S. et al., “Graphene-based composite materials”. Nature, Vol. 442, 2006, p. 282.
49. Meyer, J.C. et al. The structure of suspended graphene sheets. Nature, Vol. 446, 2007, p. 60.
50. Landau, L. D. and Lifshitz, E. M. Statistical Physics, Part I. Pergamon Press, Oxford, 1980.
51. Mermin, N. D. Crystalline order in two dimensions. Phys. Rev., Vol. 176, 1968, p. 250. 52. Shaffique Adam et al, “A self-consistent theory for graphene transport”; http://www.pnas.org/content/104/47/18392.full 53. Barras, Colin, “Atom-thick carbon sheets set new strength record”, New Scientist; http://www.newscientist.com/article/dn14354-atomthick-carbon-sheets-set-new-strength-record.html
54. Baladin, Alexander A., “Superior thermal conductivity of single layer graphene”, Nano Letters, Vol.8, No 3, 2008, p. 902.
55. Jacoby, Mitch, “Graphene´s thermal conductivity”, Chemical and engineering News; Vol. 88, No. 15, April 2010, p. 5.
56. Scarpa, F., S. Adhikari and A Srikantha Phani, “Effective elastic mechanical properties of single layer graphene sheets”, Nanotechnology, Vol. 20, 2009, p. 1; http://iopscience.iop.org/0957-4484/20/6/065709/pdf/0957-4484_20_6_065709.pdf 57. Bunch, Joseph Scott, Mechanical and electrical properties of graphene sheets, Ph. D. Thesis, University of Cornell, Ithaca, 2008, p. 15. 58. Gao, Yuanwen and Peng Hao, “Mechanical properties of monolayer graphene under
tensile and compressive loading”, Physica E: Low-dimensional Systems and Nanostructures, Vol. 41, No. 8, August 2009, p. 1561. 59. R, Rasuli, Iraji Zad A, Ahadian M. M., “Mechanical properties of graphene cantilever from atomic force microscopy and density functional theory”, Nanotechnology. May 7, 2010, p. 18. 60. Dubay, O. and G. Kresse, “Accurate density functional calculations for the phonon dispersion relations of graphite layer and carbon nanotubes”, Phys. Rev. B, Vol. 67, No. 3, 2003. 61. Kitipornchai, S, He X. Q. and Liew K. M., “Continuum model for the vibration of multilayered graphene sheets”, Phys. Rev. B, Vol. 72, No. 7, 2005.
62. Despres J. F., Daguerre E, Lafdi K., “Flexibility of graphene layers in carbon nanotubes”. Carbon, Vol. 64, No. 33, 1995, p. 87
63. Thurston, R. N. and K. Brugger, “Third-Order Elastic Constants and the Velocity of Small Amplitude Elastic Waves in Homogeneously Stressed Media”, Phys. Rev. A, Vol. 133, 1964, p.1604.
64. Liu, P. F., M. Ming, and J. Li, “Ab initio calculation of ideal strength and phonon instability of graphene under tension”, Phys. Rev. B, Vol. 76, 2007.
65. Roopam, K. et al, “Coupled quantum mechanical/molecular mechanical modeling of the fracture of defective carbon nanotubes and graphene sheets”, Phys. Rev. B, Vol. 75, 2007. 66. Lee, Changgu et al, “Elastic and frictional properties of Graphene”, Phys. Status Solidi B, Vol. 246, No. 11–12, 2009, p.2562 67. Lee, C.; Wei, X.; Kysar, J. W.; and Hone, J. “Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene” Science, Vol. 321, 2008, p. 385.
68. Castro Neto et al, “The electronic properties of graphene”, Reviews of Modern Physics, Vol. 81, Jan – March 2009, p. 109.
69. Dubois, M., Z. Zanolli, X. Declerck, and J.-C. Charlier; “Electronic properties and quantum transport in Graphene-based nanostructures”, Eur. Phys. J. B, Vol. 2, No. 71, 2009, p. 1 70. Chigo Anota, Ernesto, “Análisis DFT de las propiedades electrónicas de las hojas de grafeno y de nitruro de boro dopadas”, Superficies y Vacío, Vol. 22, No. 1, 19-23, marzo de 2009, p. 19.
71. Stephan et al., “Doping Graphitic and Carbon Nanotube Structures with Boron and Nitrogen”, Science, Vol. 266. No. 51919, December 1994, p. 1683.
72. Uchoa, Bruno and A. H. Castro Neto, “Superconducting States of Pure and Doped Graphene”, Phys. Rev. Lett. Vol. 98, No. 146801, 2007; http://prl.aps.org/abstract/PRL/v98/i14/e146801 73. Li, X. S. et al, «Large-area synthesis of high-quality and uniform graphene films on copper foils», Science, Vol. 324, 2009, p. 1312. 74. Bae, Sukang et al, “Roll-to-roll production of 30-inch graphene films for transparent electrodes”, Nature Nanotechnology, No. 5, 2010, p. 574. 75. Dikin, Dmitriy A. et al, “Preparation and characterization of graphene oxide Paper”, Nature, Vol 448, 26 July, 2007, p. 457. 76. Valencia G., Asdrúbal, “Doce temas actuales en la ciencia e ingeniería de materiales”, Informetal, No.58, 2010, p. 8.